对运输汽车的衡称重采样点确定过程的优化,能够有效提高汽车的衡称重的精度。对地磅称重采样点的确定,需要 筛除衡称重过程的粗大误差,利用平方根矩阵对称重采样点进行优化,完成衡称重精度的优化。传统方法先推导出称重测 量系统传递函数关系,并进行了离散化处理,但忽略了对称重采样点进行优化,导致精度优化效果不理想。提出基于采样点 自适应确定优化的运输地磅称重方法,首先计算运输地磅称重时的位置误差,并利用最小二乘法进行拟合求解;然后计 算运输汽车的定位误差相似度和标准差,去除冗余信号;最后利用3»准则筛除运输地磅称重的粗大误差并进行求和,取 平均值作为经过称台的运输汽车轴重测量值;在此基础上,利用平方根矩阵对运输地磅称重的基础采样点进行优化。仿 真结果证明,所提方法能够提高运输地磅称重的精度,对车辆运输的现代化管理具有重要意义。
1.引言
随着我国经济的持续增长,道路工程和物流运输业等得 到了推动性发展性,然而伴随着交通事故的频发,其中车 辆超速、超载行驶问题成为事故发生的主要因素。由于车 辆超载等一系列问题的产生,对人们生命财产安全和道路等 公共设施构成了极大威胁H。运输汽车衡称重管理系统是 测量车辆轮胎受力并计算其重量的过程H。为了促进车辆 运输的现代化管理,降低车辆的超载对路面造成的破坏,需 要对运输汽车衡称重方法进行研究。传统的基于过采样技术的运输汽车衡称重方法,首先对车辆的运动状态以及 动力特性进行分析;然后对运输地磅称重采样数据进行采 集,利用过采样技术处理采集到的汽衡称重数据;最后利用 硬件电路系统实现对车辆的称量。存在测量误差率较大的 问题,为了获得高精度的运输汽车衡称重值,成为了相关人 士的重点研究课题,为此提出了许多较为有效的方法。
文献通过分析运输地磅称重力学模型,推导出运 输地磅称重测量系统传递函数关系,并进行了离散化处 理;然后利用最小二乘法估计运输地磅称重测量系统的模 型参数,进而推算出运输汽车的实际重量。该方法存在运输地磅称重测量精度较低的问题。文献主要利用运输汽 车衡称重径向基函数神经网络逼近运输地磅称重多路传感器之间的函数关系,预测各个传感器的数据输出;然后将 各个传感器的运输汽车衡称重预测信号和实际测量信息输 入,建立信息融合运输汽车衡称重检测模型,实现运输汽车 衡称重传感器故障诊断;最后依据诊断结果获得运输汽车实 际重量。该方法由于运用了多路传感器,存在测量误差较 大、测量可靠性较低的问题。文献的运输地磅称重方法,主要利用运输汽车轴重称量,即分别测量出运输汽车各 个轴的轴重,再由测试系统计算出整个运输汽车的实际重 量。该方法由于存在许多外界干扰,容易造成测量精度较低 的问题。
针对前面阐述方法出现的一系列问题,提出一种基于采 样点自适应确定优化的运输地磅称重方法,通过仿真验 证,所提方法能够获得高精度的测量结果,具有重要的现实 意义。
2.运输地磅称重量精度优化原理
在对运输汽车进行称重时,首先计算运输汽车和称台的 振动方程,推导出汽运输汽车和称台的传递函数并进行离散 化处理;然后利用最小二乘法估计运输汽车和称台的模型参 数,进而推算出运输汽车的实际重量。
假设M表示运输汽车的质量,包括运输汽车车身的质 量Ma和运输汽车车轿的质量Mb (运输汽车轮胎质量故略不 计);K表示运输汽车和称台的刚度;C表示运输汽车和称台 的阻尼系数。则运输汽车和称台的振动方程表现为
MX + CX + KX = F (1)
式中,Z表示运输汽车和称台的振动移位,包括运输汽车车 身的振动移位又(t),运输汽车车轿的振动移位Xt (t),运输 汽车称重称台的振动移位Xit)。
假设上述式(1)中的运输汽车和称台的阻尼系数C为 零,得到两个独立的运输汽车和称台振动方程,将上述式(1) 进行Laplace变换,则运输汽车和称台输出位移量X(t)和运 输汽车和称台动态输入载荷F(t)之间的传递函数计算表达 式如下
X( t)
G( t)
F( t)
输入运输汽车和称台信号U(t)的波形在理想状态下是 个等腰梯形,则U(t)的计算公式为
u(t)=丄[r(t) - r{t - £o)-
to — £"o) + T (t — to — 2so)]
其中,r代表运输汽车和称台采样间隔;^o代表运输汽车车 轮进入和离开称重称台所用的时间;to代表运输汽车在称重 称台上行驶的时间;nt - to)代表时延为t的运输汽车单位 速度信号。在运输汽车衡称重实际测量过程中获得的是离 散信号,则上述式(3)对应的运输汽车和称台的离散传递函 数具有以下形式:
 bo + 厶1 z + b2 z + 63 z 3 + 64 z 4 + 65z 5 + b6z 6
bo + 厶1 z + b2 z + 63 z 3 + 64 z 4 + 65z 5 + b6z 6
式中,表示运输汽车和称台的Z变换系数;^1、、、 «6、bo、b、h、b3、b4、b5、b6表示运输汽车和称台的参数,由测 量结果识别获得。则运输汽车和称台的差分方程为
«1 g(n - 1) + a2g(n -2) + 03g(n -2) + 04g(n -2)
+ 05g (n - 2) + a6g (n 一 2) = 6。x: (n) + 6。
x: (n) +
厶1 x (n) + 62 x (n) + 63 x (n) + 64 x (n) + 65 x (n)
+ 66x (n) (5)
其中,(n)表示运输汽车和称台的阶跃输入,即离散化的运 输汽车重量序列;当n名6时
g(n -2) = g(n - 3) = g(n -4)
=g(n -5) = g(n -6) = g(n) (6)
由于运输汽车垂向位移x; (n)与运输汽车和称台的传感 器信号输出v(n)成正比,则
g (n) = 6'ov (n) + 6'1 v (n - 1) + 6'2v (n - 2) + 6'3v (n -3)
+ 6'4v (n-4) + 6'5v (n-5) + 6'6v (n-6) + w (n) (7)
式中,《(n)表示运输汽车称重环节引入的误差,6\v表示噪 声利用最小二乘法估计模型参数。利用上式(7)即可实现抑 制测量噪声的目的。
利用最小二乘法估计上式(7)中的参数6';v,计算g (n) 取平均值获得运输汽车的实际重量。
综上所述为运输汽车衡称重的采样点姿势运营确定方 法原理,根据此原理完成对汽车衡称重精度的优化。
3.运输地磅称重量精度优化方法
3.1基于采样点自适应确定的信号采集和分析
首先计算运输地磅称重信号和运输汽车运动学方程; 然后计算运输汽车的位置误差,并利用最小二乘法进行拟合 求解;最后利用空间差值原理,计算运输汽车的定位误差相 似度。具体步骤描述如下
假设m(t')表示运输汽车轴重的真实信号;n' (t')表示 伴随运输汽车轴重真实信号m(t')的噪声;则运输地磅称 重信号y (t')表示为
y( t') =m (t ) + n (t ) (8)
其中,运输汽车轴重真实信号m(t')可以表示为 {M'汽车轮胎压上称台 {o 其余
式中,M'表示运输汽车某个轴的轴重真实值。
假设人表示运输汽车相邻两个轴之间的空间变换关 系,利用采样点自适应确定方法建立的J自由度运输汽车运 动学方程表示为
7J = A1A2 …冷 (1o)
其中
= rot (z',) trans (z', ) trans (x, a;) rot (x, a;) rot (y,,;) (11)
式中,化表示运输汽车运动学参数。运输汽车的 位置误差可以用运输汽车运动学参数误差的线性组合形式 表示Ap = J1 AOi + J2 Adt + J3 Aat + J4 Aa; + J5 (12) 式中,A(9;、Adi、Aa;、Aa;、AS;表示第i个轴的运输汽车运动 学参数误差。
将上式化简可得
Ap = J- Ap (13)
其中,Ap表示运输汽车的运动学参数误差向量。采用最小 二乘法进行拟合求解可得
Ap = (JTJ) 1JT Ap (14)
根据上式计算获得的运输汽车运动学参数误差可以估 计运输汽车上称台的定位误差。
则运输汽车的定位误差相似度计算表达式为
1 N( h)
r(h) = 2^g [ Ap(e{i')) - Ap(e{i') +h) ]2 (15)
式中,e'~ i')代表运输汽车衡称重时第r个采样点的轴输入;Ap (e{ i))代表该采样点对应的运输汽车衡称重实际测量定位误 差;h代表运输汽车轴空间中两个轴输入的分割量,即轴输 入在轴空间中的欧氏距离;(e{i) + h)代表与的分割量为 h的轴输入;N(h)代表满足分割量为h的点对的个数。
利用空间差值原理,运输汽车目标点pl0)的定位误差估 计值可以用已知采样点的定位误差线性组合表示,其表达式 如下
a p^ =乏一')Af (16) i = 1
式中,A^,(0)表示运输汽车目标点pl0)在*轴上的定位误差 估计值,在y轴和z上的定位误差估计值计算同理;w'f'表示 运输汽车目标点Pw在*轴上的权重;Ap':i')表示采样点pi') 在:轴上的的定位误差真实测量值;在y轴和z轴上的相关 参数计算同理。
3.2基于采样点自适应确定的信号处理
依据3. 1节对运输汽车的定位误差相似度计算结果,首 先计算运输地磅称重标准差,去除运输汽车经过称台时的 冗余信号;再利用3£准则筛除运输汽车衡称重的粗大误差, 并对筛除粗大误差后的信号进行求和,取平均值作为经过称 台的运输汽车轴重测量值。详细操作过程如下:
假设对被测量运输汽车进行等精度测量,获得独立的测 量值&,2,其算术平均根为
,珋=士 X:i (17)
n i = 1
则运输汽车定位剩余误差为
vi = :i -X (18)
按照贝塞尔公式计算运输汽车衡称重标准差,其表达为
e = lin /— g (:i -x)2 (19) 一槡 n
假设运输汽车衡称重的某个测量值表示为的剩余误 差vt (1 ^b^n),且满足以下条件
I = \xb -X I > 3 (20)
则判断Xb是包含粗大误差的坏值,应该筛除,将筛除后的运 一 78 — 输地磅称重剩余数据继续采用3e准则,直到将所有获得 的坏值筛除为止。
根据上述式(20),将运输地磅称重数据筛除粗大误差 后的数据进行求和,取平均值作为经过称台的运输汽车轴重 测量值,完成基于采样点自适应确定的运输汽车衡称重。
3.3运输地磅称重采样点自适应确定方法优化
根据运输地磅称重精度补偿的应用需求,在3. 1节运 输汽车衡称重信号采集的基础上,分析运输汽车衡称重最优 采样点具备的特征;然后计算运输汽车衡称重的最优采样点 数学模型;最后利用平方根矩阵对运输汽车衡称重的基础采 样点进行线性变换得到滤波采样点,实现采样点自适应确定 方法的优化,具体过程描述如下:
分析运输汽车衡称重最优采样点具备的特征:
1)采样点个数最少;
2)最优采样点能够使得运输汽车所有目标点在精度补 偿后的剩余误差之和最小;
3)最优采样点需要在指定的工作范围内选择;
4)最优采样点需要使得运输汽车衡称重时的各个目标 点在精度补偿后的剩余误差在给定的精度要求区间内。
根据上述分析,运输汽车衡称重的最优采样点数学模型 计算公式如下
min/1 = Q (21)
L
minf2 = g I Ap, - Ap^ 1 (22)
i'=1
「1 在 e(i')在 ru
s. t. { u (23)
11 a, - ApUi') 1 在 s
式中,<?表示运输地磅称重最优采样点集合包含的元素数 目;L表示运输地磅称重目标点(待精度补偿点)的数目; Ap:']表示运输地磅称重目标点在精度补偿前的原始定位 误差;运输汽车衡称重目标点在精度补偿后的剩余误差大小 表示为| ApM - ApU:') ;r1和r“分别表示运输汽车各个轴角 的上下限约束,是运输汽车衡称重的空间范围;s表示运输地磅称重实际工程应用中的定位精度要求。
根据上述计算,利用平方根矩阵对运输汽车衡称重的基 础采样点进行线性变换得到滤波采样点,其表达式为
^i = DkUk 槡A7槡7槡^qt (24)
其中,槡7表示运输汽车衡称重协方差矩阵qk的平方 根矩阵。
将上述式(23)和(24)相结合,即可实现运输汽车衡称 重采样点自适应确定方法的优化。
4.仿真结果与分析
仿真的实现采用Visual C++和Matlab7. 0混合编程,实 验将传感器与信号测量系统进行并联,对运输汽车衡称重称 台的实际采集信号进行处理,其中信号采集利用单片机,信号采集频率为300Hz。实验数据来源于某运输地磅称重 系统称台采集到的5000个信号,随机选取其中2500个进行 仿真。
利用采样点自适应确定方法采集的运输汽车衡称重信 号含有多种噪声成分,其波形如图1所示。
根据图1可以看出,利用采样点自适应确定方法采集的 运输汽车衡称重信号由于包含了较多的噪声成分,使得采集 到的信号幅值最高为0. 9左右,最低在0. 5,误差较大,容易 造成运输汽车定位精度不高,从而导致实际称重误差较大的 问题。
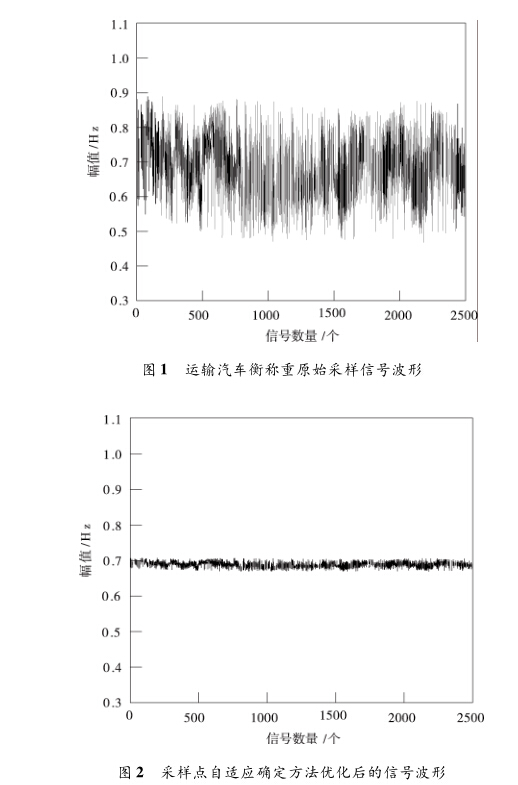
从图2中可以看出,利用平方根矩阵对运输汽车衡称重 的基础采样点进行线性变换得到滤波采样点信号很好地抑 制了噪声影响,将采集到的信号幅值均控制在0. 7的范围 内,大大改善了信噪比,为后续提高运输汽车称重精度提供 了良好的数据基础。
为了进一步验证所提方法有效性,采用文献、文献 方法与所提方法优化前后的运输汽车称重误差率(% ) 进行对比分析,对比分析结果如图3所示。
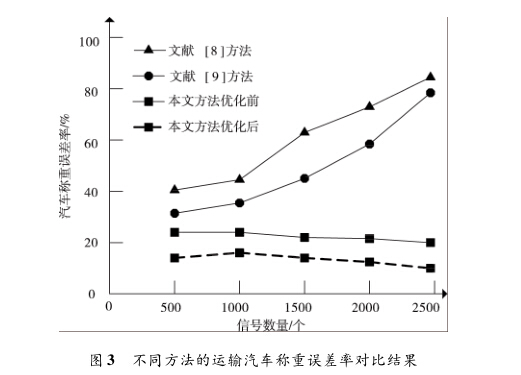
定义运输汽车称重的误差率计算公式
户生古地磅称重测量值-汽车实际重量..inn~ 误差率= 汽车实际重量 x
从图3中可以看出,文献H方法的运输汽车称重误差率最 大;文献9]方法的运输汽车称重误差率次之;所提方法采用 的采样点自适应确定方法的运输汽车称重平均误差率为 20%左右,且误差率相对平稳;采样点自适应确定方法优化 后,将运输汽车称重误差率降低到了 10%以内,在运输地磅称重管理系统,这样的误差率几乎可以忽略不计,说明了 所提方法优化后的有效性。
5.结束语
采用当前方法对运输汽车进行称重时,测量误差较大, 为此提出一种基于采样点自适应确定优化的运输地磅称 重方法,仿真结果结果验证了该采样点优化方法的有效性, 对减小称重误差率具有良好的实用价值。



